Proč něco existuje místo aby neexistovalo nic? (jakože něco reálného s nějakými vlastnostmi a ne blbosti jako množina neexistujících věcí nebo krabice z níž jsme vyndali i logiku s matematikou)
My si pojmy existence či realita spojujeme s nějakými geometrickými a topologickými vlastnostmi dotyčného objektu a prostoru v němž se nachází. A domníváme se, že Nic žádné takové vlastnosti mít nemůže, tudíž tu musí být nějaké Něco odlišné od Nic.
Jenže Nic je potvůrka podivná a za určitých podmínek to dokáže, takže původní otázka vlastně nemá smysl, protože kromě Nic a imaginárního Méně než nic objektivně skutečně nic neexistuje.
O tom jak to Nic dokáže je vlastně skoro celý zbytek tohoto webu. Tady jen uvedu pár zajímavých vlastností a schopností Nic, aby bylo jasné že nevařím z vody.

Jak už bylo uvedeno, Nic nemá žádného objektivního pozorovatele. A nemá ho mimo jiné proto, že nemá ani hranici, která by ho od něj oddělovala geometricky ani logicky. Dokonce ani nic není mimo Nic, nýbrž je jeho součástí.


Nic je tak jak je, nedá se objektivně prakticky nijak popsat. Naopak všechny naše základní pojmy jako (ne)existence, (ne)realita, jednoznačnost či paradox jsou obrazem různých možností jimiž se Nic může či nemusí uzavírat do sebe.
Nic lze tedy pozorovat jen z perspektivy nějaké jeho části "pozorující" zbytek. Co tedy tato část Nic "uvidí a neuvidí"?

Uvidí, že zbytek Nic jsou různé vzájemě se vylučující možnosti, nekonečně vnořené "koláče" či "stromy" dílčích nic, jenž se vzájemně překrývají, obsahují a hlavně vylučují.
Dvě Nic se vždy liší o další Nic (říkám tomu Neztotožnění). Proto pokud jsou někde v těch koláčích či stromech dvě (či více) zcela identické dílčí struktury (jenž jsou samozřejmě také Nic), nejde o dvě (či více) Nic, nýbrž jedno Nic na dvou (či více) místech.
Tomuto stavu říkám Ztotožnění a má zásadní význam pro vznik konečných, uzavřených a jednoznačných možností Nic v nichž mohou vznikat iluze. Podrobněji k Ztotožnění a Neztotožnění zde.


***Old but gold
Pokud jsou v možnosti Nic Ztotožněny všechny nejnižší uzly či "matrjošky", vznikne struktura, kterou už lze pokládat za realitu. Těmi se také budeme nadále asi z 90% zabývat.
Taková struktura už bude mít topologicko-geometrickou interpretaci a tudíž v jejích nízkodimenzionálních projekcích mohou být přítomny různě složité iluze. Včetně iluze času, života, vědomí.
Old but gold***
Celé je samozřejmě naprosto statické, skutečný čas (a s ním skutečná změna nějakých vlastností a parametrů) se do toho nemá jak dostat.

Neuvidí v těch strukturách samo sebe (svou strukturu), protože je to pohled z jeho perspektivy a v ní kvůli Ztotožnění (viz pár řádků výše) žádné kopie neexistují. A neuvidí žádné pozadí (např. prostor) v němž to celé je, protože Méně než nic je virtuální záležitost.
Bez skutečného času samozřejmě neuvidí ani žádnou změnu či pohyb. A neuvidí ani modrý traktůrek jak si dělá brum brum na poli. Tyhle "reálné" věci vznikají až filtrováním v složitých iluzích. Nic rozhodně není všechno ani neobsahuje všechno.


Poznámka 1: Ve fyzice je vlastně právě "naivní Nic jako bod bez vlastností" oním virtuálním pozorovatelem, kterého lze kamkoliv umístit i s jeho vztažnou soustavou, aniž by jakkoliv ovlivňoval zkoumanou realitu...
Poznámka 2: Realita jako kombinace Ztotožnění a Neztotožnění dost připomíná násobení vlnové funkce její komplexně sdruženou funkcí v kvantové mechanice.

Poznámka 3: Jak dostaneme na čistý papír nějakou informaci bez tužky? Zohýbáme ho. Představme si nekonečně tenký papír a máme dobrou představu jak Ztotožněními vzniká geometrická realita z Ničeho.


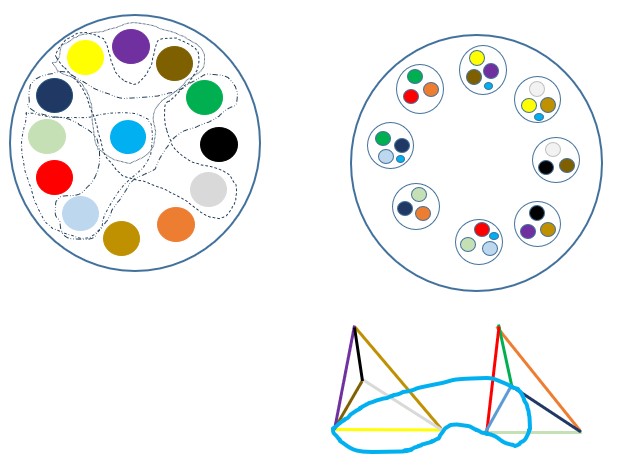
Vzhledem k negeometrickým vlastnostem možností Nic každé zobrazení silně kulhá, dokonce i pro velmi malé a idealizované možnosti. Můžeme si třeba představit Nic jako 8 Nic z nichž každé dále obsahuje 3 Nic. A k tomu stanovit, že skutečných Nic není 24,
nýbrž jen 12, protože vždy 2 jsou "Ztotožněna". (na obrázku vpravo - pohled na "strom" či "matrjošku" shora, páry Ztotožněných Nic jsou vždy stejnou barvou)
Nebo naopak vyjít z těchto dvanácti Nic a na nich vytvořit 8 vzájemně se překrývajících tříčlených skupin. (na obrázku vlevo)
Na obrázku dole pak vidíme, že to dá interpetovat jako jakási pokroucenina, která se dá sice nakreslit, ale nemůže v našem "normálním" dimenzionálním prostoru existovat. Asi jako ten Penrosův trojúhelník v úvodu.
Navíc délka hran je ve skutečnosti nulová, protože vyjadřují Ztotožnění. "Sousedství" dvou uzlů ve skutečnosti znamená sdílení nějaké abstraktní vlastnosti.


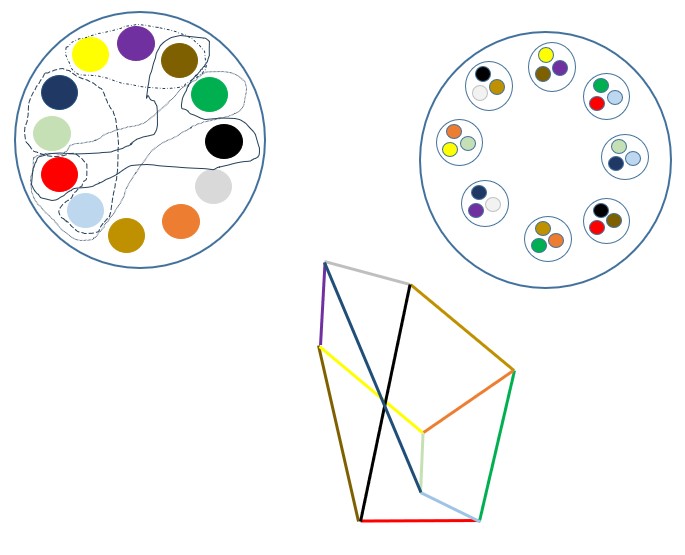
Velmi vyjímečně nastane případ, kdy kombinace "správné" struktury možnosti Nic (díky "správným" Ztotožněním dílčích Nic) vytvoří něco, co se dá reálně geometricky interpretovat. Třeba jako krychle.

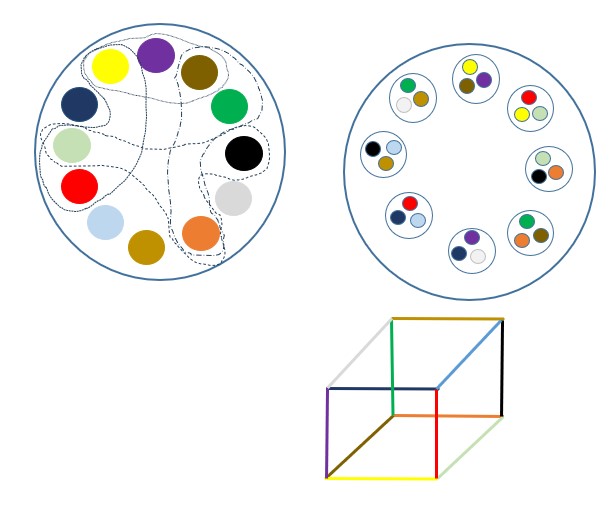
Může se stát, že celý útvar je geometricky absurdní, ale některé její části nižších dimenzí jsou mají geometrickou interpretaci - viz příklad výše před "krychlí".


Může dokonce nastat případ, kdy touto interpretací je několik oddělených geometrických útvarů.


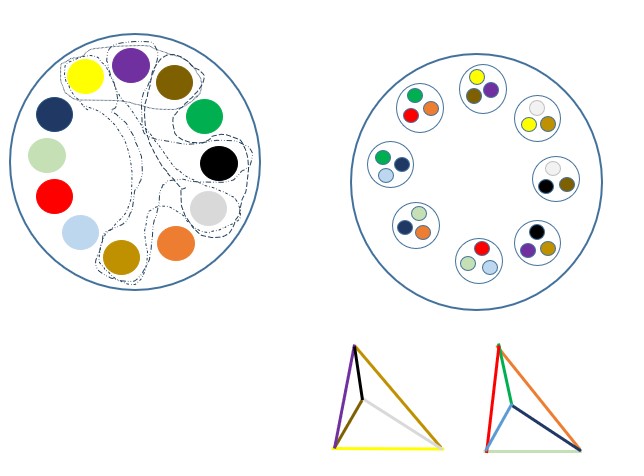
Většina možností je samozřejmě daleko mimo jakýkoliv popis a interpretaci. Co je například tohle ?!


Na druhou stranu existuje řada možností Nic, které jsou sice nereálné a nezobrazitelné, ale po větším či menším doplnění z nich něco reálně geometrického vzniknout může. Jako v tomto případě, kdy byly z "krychle" odebrány 2 hrany.


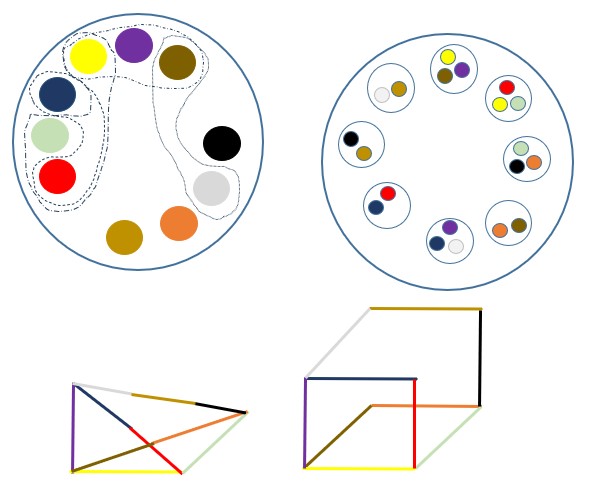
Je zřejmě, že lze i naopak jakkoliv složitý geometrický útvar vyjádřit jako takovouto kombinaci "stromu" či "matrjošky" a Ztotožnění. Obrázek snad kreslit netřeba...


V některých případech je názornější si výsledný geometrický útvar nepředstavovat v jeho skutečné vysoké dimenzi (což lze vždy), nýbrž jako propojení několika nízkodimenzionálních útvarů. Malý počet mnohonásobně Ztotožněných Nic plní lépe roli vlastností
jednodušších útvarů než mnoha jejich dodatečných dimenzí.




Ačkoliv Nic je pořád stejné, v interpetacích může zaujímat roli bodů, hran, ploch atd. Nebo i vlastností, viz příklad výše. Zde je zase krychle, tentokrát jako seskupení svých stran místo hran a bodů.



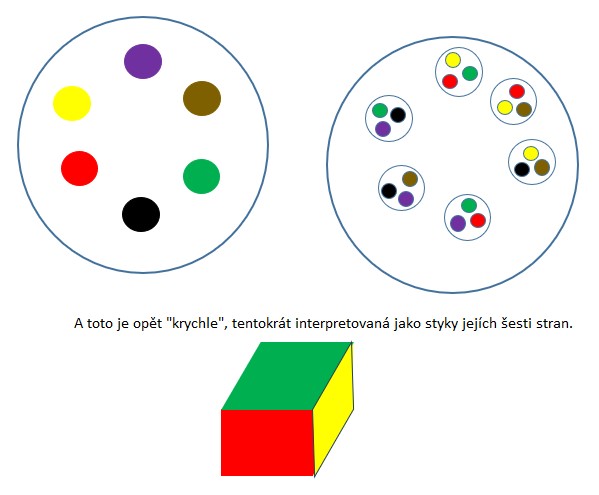
Docela to připomíná védantický "brahman", neměnný ale "poblikávající" různými pomíjivými možnostmi a v nich se tvořícími iluzemi.

Nic bez vlastností se mohou buď shodovat (zelené čáry) nebo lišit (červené čáry). Díky absenci vnějšího pozorovatele nemusí být tyto struktury ani logické, ani reálné (uzavřené).
"Obláčky" jsem použil jako zdůraznění, že Nic rozhodně nejsou body.



A taky to připomíná "kvantové tunelování" při němž částice reprezentovaná vlnovou funkcí prochází v nereálné podobě potenciálovou bariérou a poté se opět stává reálnou.

Moje původní představa instance Nic je tady. Měl jsem tehdy ještě problém s tím, že končí v Méně než nic a že její vztah ke geometrickým útvarům není tak přímočarý jak by se mi líbilo. Také jsem se domníval, že i původní
"velké nic" je obklopeno Méně než Nic, což není pravda, protože je definováno jako součet těch menších, na které se ten problém tedy přenáší.

Zpět na úvodní stránku