Třístupňový model možnosti Nic
Třístupňový model možnosti Nic (a jeho některá rozšíření)
Tento model modeluje konečnou, jednotnou a jednoznačnou možnost Nic s již danými Ztotožněními. Případná nejednoznačnost popisu nebo rozpad možnosti Nic na několik oddělených je proto chybou modelování,
ne nejednoznačností možnosti Nic. Možnost Nic také musí být uzavřená, to znamená, že všechna její "nejnižší Nic" jsou Ztotožněna nejméně do dvou dílčích Nic této možnosti. To nebrání tomu, aby tato možnost Nic
byla součástí ještě většího útvaru s jejich dalšími Ztotožněními. Touto uzavřeností se celá možnost Nic liší od svých částí, které naopak uzavřeny být nesmí, protože by to porušovalo požadovanou jednotnost
možnosti Nic. Teoretická "prostě Nic" nebo "zcela lichá Nic", která se nikam Neztotožňují jsou v rámci tohoto modelu ignorována. Tato modelová omezení samozřejmě netvrdí, že všechny vzájemně se vylučující varianty
celého paradoxního Nic splňují tato omezení. Jde o to věnovat se jen tomu, v čem mohou být za splnění dalších mnoha podmínek komponenty naší iluzorní reality - prostor, geometrie i "Já".
Pro připomenutí 4 hlavní "axiomy":
1. Nic nemá objektivního (=vnějšího) pozorovatele
2. Nic může obsahovat libovolný počet různých! Nic (Korektně řečeno, Nic může být reprezentováno libovolným počtem různých! Nic. Korektně by tedy místo "koláčů" měly být používány teselace - trojúhelníky, čtverce,6úhelníky...)
3. Nic může být obsaženo v libovolném počtu různých! Nic (tedy se do nich promítat). Alternativně lze říci, že každé nejnižší Nic (které už žádná svoje vnitřní Nic nemá) může být totožné s libovolným počtem
dalších "nejnižších Nic". Pro vyšší Nic to platí jen když se shoduje jejich struktura nižších Nic až po ta nejnižší. To je ale jen nutná podmínka - pro případ že takové Ztotožnění opravdu chceme modelovat.
To vyplývá z toho, že jakákoliv část Nic může být totožná s jakoukoliv jinou částí Nic nebo dokonce s celým paradoxním Nic (tuto možnost ovšem tenhle model neřeší).
4. Nic se od sebe vzájemně liší svými vnitřními Nic - jejich počtem a tím, s kterými dalšími Nic je spojují. (pokud se tedy liší a nejsou jen projekcemi podle bodu 3)
Terminologie
Velká elipsa samozřejmě vyjadřuje celou možnost Nic. Ta je zde reprezentovaná jako 18 Nic, nazývejme je třeba dílčí nebo (pro)střední. V odpovídající (pseudo)geometrii vlastnosti Nic odpovídají jednotlivým bodům
či vrcholům, v nichž se kombinují abstraktní vlastnosti. Každé z nich je reprezentováno několika Nic, která tu nazývám vnitřní, nejnižší či Ztotožněná Nic a jenž jsou vyjádřená nejmenšími kroužky. Zde jich je 72.
Násobnost jednotlivých Ztotožnění budu nazývat jejich abstraktními vlastnostmi (av).
Formalismus
Dále budu používat následující formalismus třístupňového modelu: {18bodů{1x6,4*5,7x4,6*3},10av{ztot.do:12,10,8,8,6,6,6,6,6,4}}. První číslo obsahuje počet prostředních Nic a za ním v závorce počet "nejnižích Nic",
jak je jednotlivá prostřední obsahují Nic, tedy jejich dimenzionalitu. Následuje počet abstraktních vlastností (av) v dané možnosti Nic a v závorce za nimi pro každou z nich násobnost tohoto Ztotožnění.
Součty kusů (v příkladu zde 72) v obou závorkách se musí rovnat. Takto je možnost Nic jednoznačně popsaná.
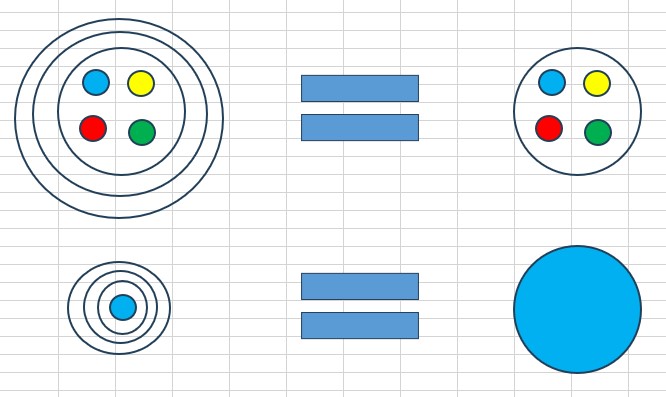
Krok 1: Vezmeme možnost Nic ve formátu "Vnořené koláče". Samozřejmě nic nevybíráme protože tam nejsme. Je to prostě jedna z možností, ostatní jsou jí rovnocenné, jen je tu zrovna nepitvám.
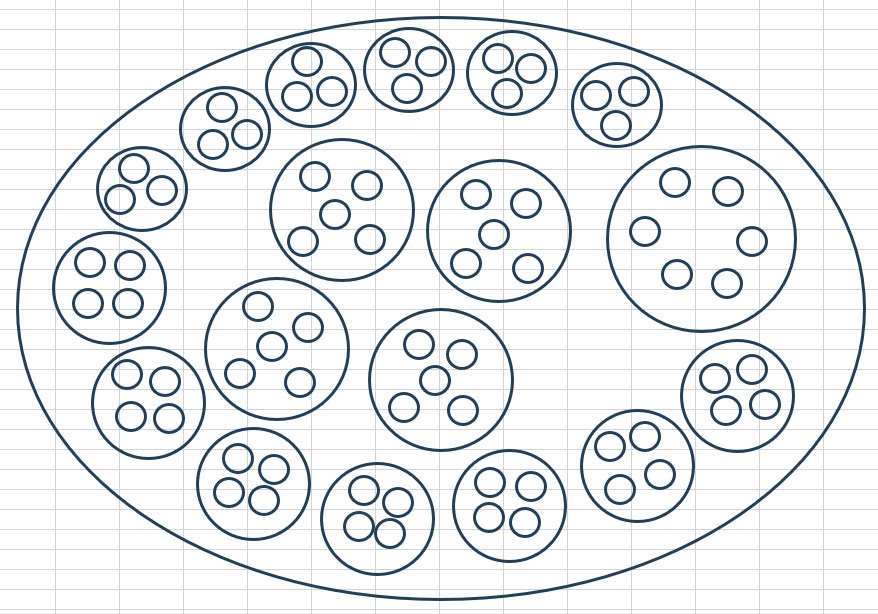
Krok 2: Zvolíme mapu všech Ztotožnění v této možnosti Nic. Opět nic nevolíme, jako v Kroku 1. Nějaké slovní obraty se použít musí.
Ztotožňujeme samozřejmě pouze "nejnižší Nic", která už žádné menší "koláčky" v sobě neobsahují.
Ztotožnění těch vyšších vznikají případně až sekundárně, pokud se jejich vnitřní struktury zcela shodují a to Ztotožnění opravdu v možnosti Nic je, tj. souhlasí nejen počty "koláčků" ale i jejich modelové barvy.
Jinak stejná struktura neznamená automaticky Ztotožnění. Nejmenší kroužky jsou ostatně také všechny "stejné", ale Ztotožněné do 10 Nic...
Aplikace této mapy Ztotožnění na "Vnořené koláče" dané možnosti Nic musí splňovat jen následující podmínky, pokud je nesplňuje vrať se na Krok 2:
Podmínka 1: Neopakují se stejně složená dílčí Nic. Jednou jsem zvolili, že možnost Nic je třeba z deseti různých dílčích Nic tak tam nebude žádné dvakrát ab, dgf, cgih, ehi, ... fgh, fgh!
Podmínka 2: Neopakují se stejná Ztotožnění do jednoho dílčího Nic. Žádné aab, beeeec, ffgg atd.
Podmínka 3: Žádné Ztotožnění není do všech dílčích Nic dané možnosti. Žádné abc, akl, axy, acu...., amn.
Podmínka 4: Žádné Ztotožnění nedubluje jiné ve všech svých výskytech. Žádné abc, abde, abkl, abijt...., abxy.
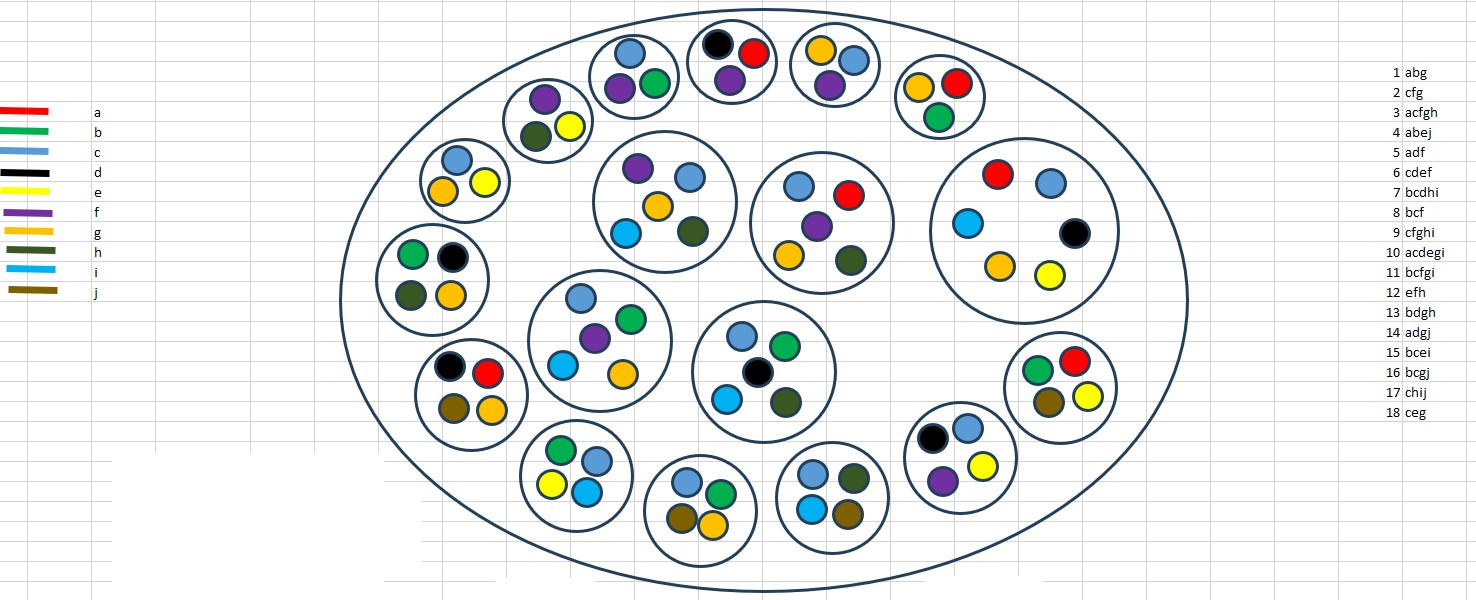
A toto je již finální třístupňový model zadané možnosti Nic. Má až 12 dimenzí a v úsečkové projekci by vyžadoval 248 úseček.
Co když ale možnost Nic skutečně obsahuje více než 3 stupně?
Potom mohou nastat dvě možnosti:
1. Z elementárních abstraktních vlastností a,b,c,.... j se stanou složené, a=ABC, b =DEFG, ... j=XYZ, ale jejich nové elementární vlastnosti budou jedinečné pro každou nově složenou vlastnost.
Nebude žádné a= ABC, b =AEF, c= CKL,...j=ABX. Tím se ovšem na struktuře možnosti Nic oproti variantě s třemi stupni vůbec nic nezmění a ani není důvod další stupeň nějak modelovat, protože je vlastně celý
porušením výše uvedené Podmínky 4 o nedublování Ztotožnění v dílčích Nic.
2. Elementární abstraktní vlastnosti zůstanou jak jsou, ale přidá se další "mezistupeň" grupující dosavadní dílčí Nic do větších celků, ale menších než celá možnost Nic.
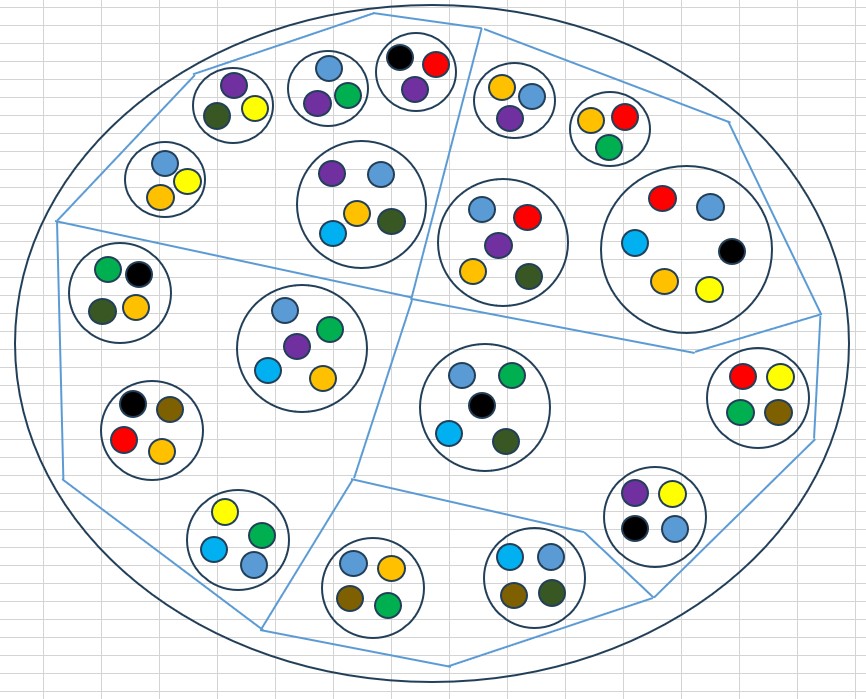
Struktura možnosti Nic zůstala pochopitelně stejná, protože Ztotožnění na nejnižší úrovni se nezměnila. Ale nyní se skládá z několika "oblastí", které obsahují každá několik bodů a svých vnitřních vlastností.
Řada vlastností je ovšem sdílená více oblastmi, což vyjadřuje, že ty oblasti spolu sdílejí některou elementární vlastnost. A mohou dokonce sdílet i složené vlastnosti. Už neplatí, že možnost Nic nesmí
obsahovat dvě stejná dílčí Nic (abc, abc, def, ceg,...). Nyní už nesmí být jen dvě zcela stejné oblasti. To umožňuje, aby existovaly obrovské možnosti Nic s jen málo elementárními abstraktními vlastnostmi.
Oblast ale také představuje "validní Nic" pro projekce, poskytující perspektivu Nic "pozoruje" svůj doplněk v možnosti Nic. Ostatní projekce jsou jen matematické kombinace nemající v dané možnosti Nic
žádný reálný význam.
Dalším zvyšováním počtu stupňů už se kvalitativně nic nemění. Dílčí oblasti se vzhledem k jejich složité (pseudo)geometrii stávají spíše komponentami než vlastnostmi. Vzhledem k tomu, že stále více bodů i
i vlastností bude obsaženo uvnitř "nejvyšších" oblastí (těsně pod samotnou možností Nic), je možné, že její dimenzionalita vyjádřená pomocí oblastí bude podstatně nižší než by byla v čistě třístupňpovém modelu.
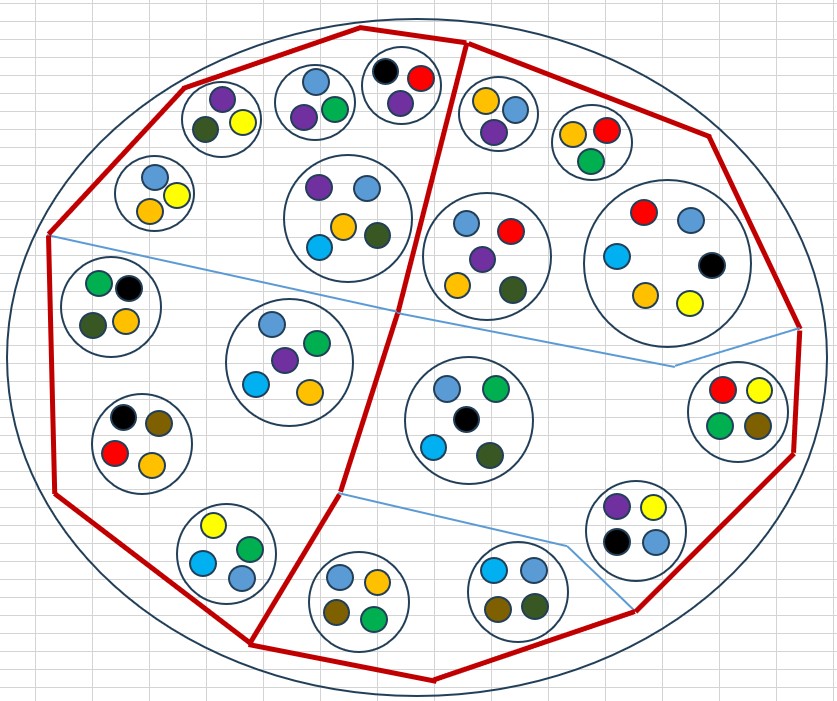
Pokud jsou Ztotožnění jen na nejnižším stupni (a není tam žádné "liché" Nic), je možnost Nic vlastně tvořená několika nezávislými menšími možnostmi Nic (což odporuje požadavku na její jednotu).
Takhle obecně asi není příliš zřejmé, k čemu je třístupňový model možnosti Nic dobrý. Náš iluzorní svět s časem, prostorem i myslí je samozřejmě velmi speciální druh možnosti Nic.
Podívejme se na možnosti, které by mu mohly být blízké.
Dočasné otázky:
1.Co se stane pokud možnost Nic obsahuje zcela oddělenou jinou možnost Nic?
2.Co se stane, pokud možnost Nic obsahuje strukturu spojenou se zbytkem mN jenom na nejnižší úrovni a nedochází k žádnému opakování vyšších vlastností a oblastí?
3.Jak fungují stupně mN v nichž nedochází k žádnému opakování a jsou vlastně jen "pojmenováním" svých obsahů na nižších stupních?
4.Co znamená nepřítomnost určitých vlastností v některých oblastech?
5.Jak funguje "kaskáda" vertikálního ztotožnění? Co když některé stupně "přeskakuje"?
6.Jak se docílí "souřadnic" a "barev" ,tj. obrovského počtu vlastností z jen několika elementárních a.v.?
7.Co vlastně "kaskádování vlastností"?
Detailní rozbor možností Nic
Některé anomálie
1. Co když možnost Nic obsahuje neztotožněná sólová Nic nebo Nic Ztotožněná za hranice této možnosti Nic?
Tak to porušuje uzavřenost a nejspíš i jednoznačnost možnosti Nic, což odporuje požadavkům popsaným v úvodu této stránky.
Vlastně by to znamenalo, že daná možnost Nic není kompletní, stejně jako nejsou kompletní její vnitřní Nic. Nedefinovaná a Neztotožněná Nic nelze ani prostě vyškrtat, ani vzájemně Ztotožnit.
Pokud jsou x a y taková Neztotožněná Nic, nelze pokládat dílčí Nic cdef a cdefx za totožná a tudíž současně nepřípustná ve stejném vyšším Nic. Ani cdefx není totožné s cdefy.
Nelze vytvářet projekce z pohledu takových Neztotožněných Nic.
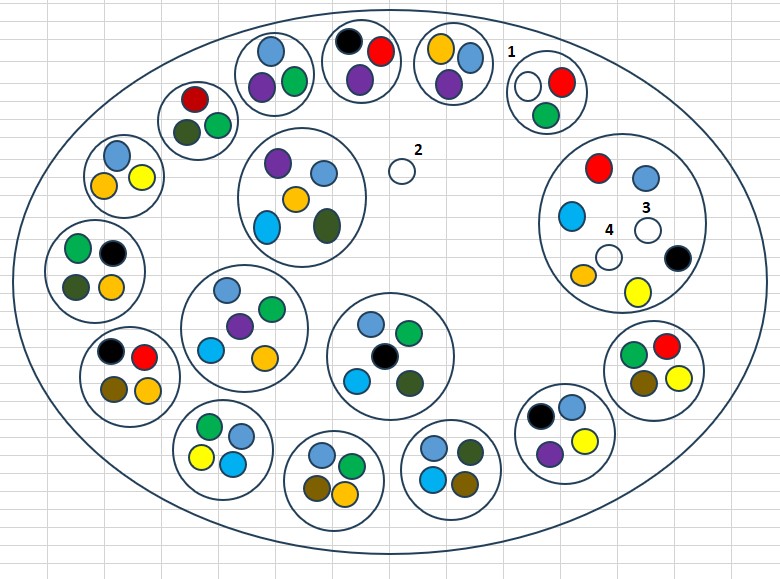
2. Co když je Ztotožnění mezi různými stupni (rekurze nebo vertikální Ztotožnění)?
Jakékoliv Nic samozřejmě může být totožné s jakýmkoliv jiným Nic. Proto je tato situace korektní a může nastat. Znamená to, že se jednoduchá abstraktní vlastnost zachovává i ve vyšších stupních dané možnosti Nic.
Může se ale projevovat jinak než na nižším stupni protože se změnil její kontext. Pokud mají různé oblasti možnosti Nic různou "hloubku" je takové Ztotožňování mezi různými stupni přímo nutné, protože jedině tak lze
udržet požadovanou uzavřenost možnosti Nic.
Vertikální Ztotožnění nemusí být jen mezi dvěma sousedními stupni možnosti Nic. Může být ve všech stupních nebo jen v některých. Z perspektivy těchto vertikálně Ztotožněných Nic pak vznikají zajímavé projekce obsahující
"pozorovatele", případně celou kaskádu "pozorovatelů" v různých kontextech.
A nemusí se jednat o elementární abstraktní vlastnost, nýbrž libovolně složitou vlastnost či oblast Ztotožněnou do ještě vyšších stupňů než kam "přirozeně" patří.
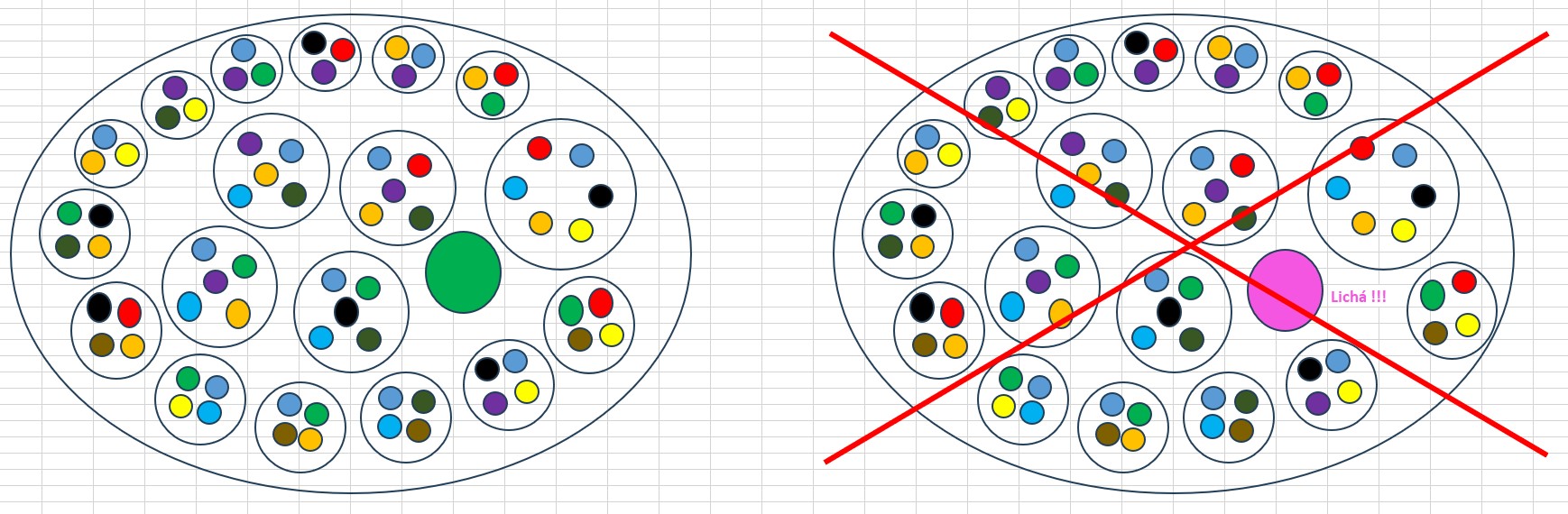
3. Co když Nic obsahuje jen jedno nižší Nic? A to pak třeba víc nejnižších Nic?
Takovýto "teleskop" je v rozporu s úvodním axiomem č.2, protože jedno Nic není různá Nic. Ani fakticky v možnosti Nic nic nemění - (pseudo)geometrii, projekce, pozorovatelské perspektivy, identičnost vůči jiným Nic....
2. Nic může obsahovat libovolný počet různých! Nic (korektně řečeno, Nic může být reprezentováno libovolným počtem různých! Nic)
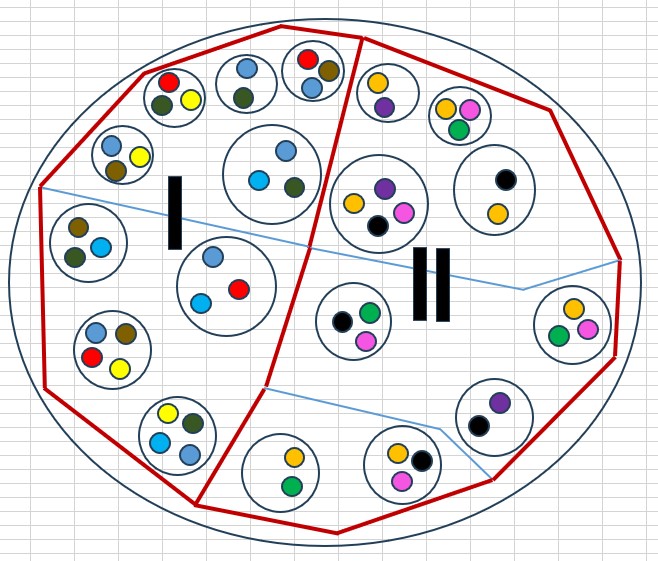
4. Co se stane pokud možnost Nic obsahuje zcela oddělenou jinou možnost Nic?
Potom mohou nastat dvě základní možnosti.
4.1 - Celá možnost Nic je už na úrovni svých nejvyšších oblastí rozdělena na dvě či více zcela oddělené části (z hlediska výskytu elementárních abstraktních vlastností, tedy v modelu barev).
Potom je jasné, že tato možnost je vlastně několik zcela nezávislých možností Nic, které nemají žádný vzájemný vztah a je třeba je analyzovat odděleně.
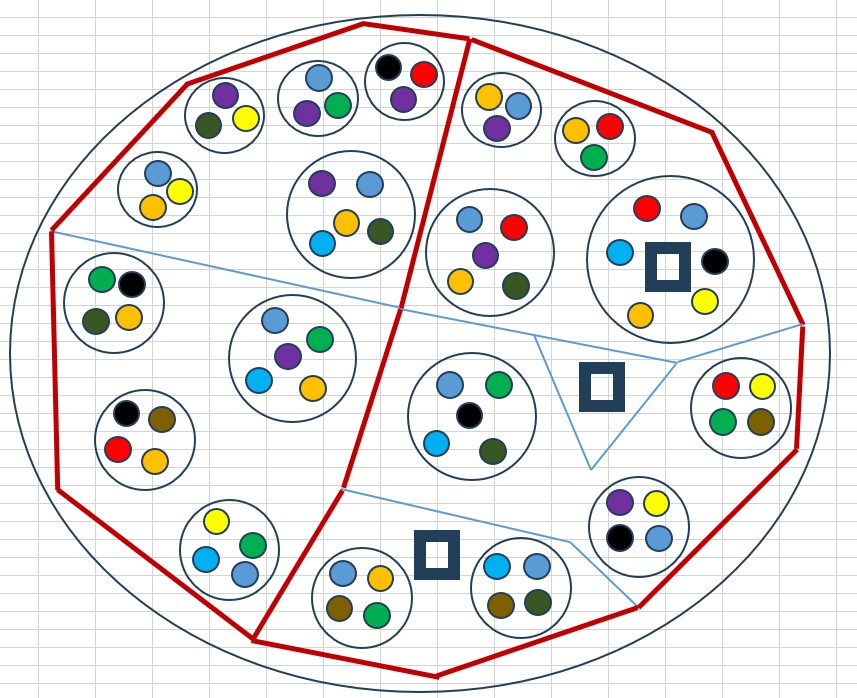
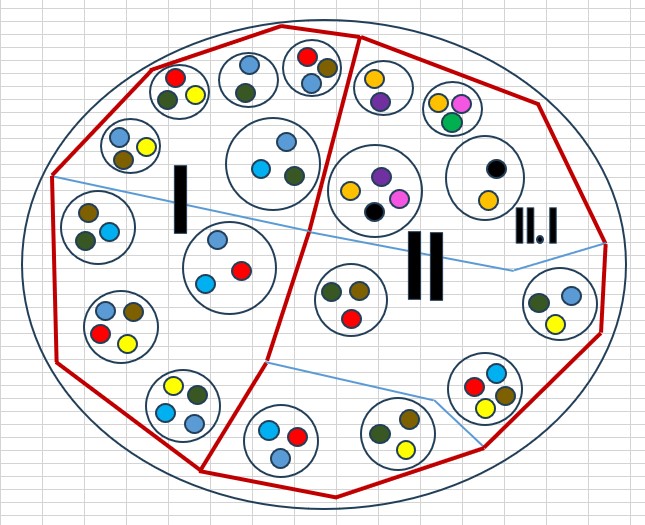
4.2 - Celá možnost Nic je rozdělena až pod úrovní nejvyšších oblastí I a II. V případě na obrázku je touto oddělenou a tedy nesouvisející oblastí II.I
Pokud jsou všechny oblasti a pod-oblasti I a II jinak korektní tak to znamená, že se v oblasti II vyskytuje zcela izolovaná struktura II.I. Není to problém jako Neztotožněná sólová Nic, protože zde se jedná o jasně definovanou
uzavřenou strukturu, která má ale zcela jiné vlastnosti než zbytek dané možnosti Nic. Něco jako "černá díra". V praxi je zajímavá situace, kdy nějaká oblast sdílí se zbytkem možnosti Nic jen vlastnosti "kódující souřadnice".
5. Co se stane, pokud v možnosti Nic dochází k opakování/Ztotožňování vlastností jenom na nejnižší či 2.nejnižší úrovni a nedochází k žádnému opakování vyšších vlastností a oblastí?
Vznikla by sice reálná (pseudo)geometrická struktura, ale nic (makroskopického) by se v ní nejen neopakovalo, ale ani si nebylo podobné. Jako bych v tom světě mohl použít každé popisující slovo jenom jednou. Totální chaos...
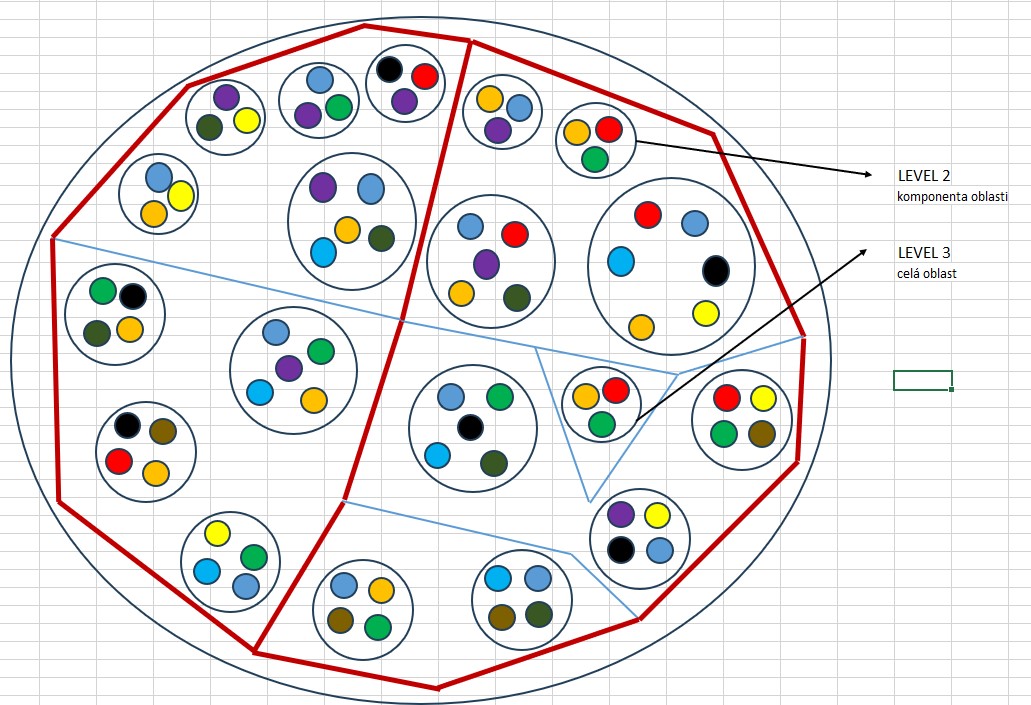
Může ovšem nastat i situace, kdy k neopakování vyšších vlastností dochází jen v oddělené oblasti (na příkladu zde Nejvyšší oblast označená Země) možnosti Nic. Ta je tím pádem chaotická a nepodobná zbytku této možnosti Nic,
ale na rozdíl od 4.2 s ní propojená na nejnižší úrovni. Zbytek mimo "Zemi" může vytvářet (pseudo)geometrické struktury vyššího řádu, zatímco "Země" k tomu dodává jen chaos s nejnižšími částicemi nebo jen "souřadnicemi".
Zpět na úvodní stránku