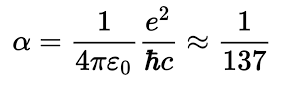Záhadné rovnice
Einsteinovu slavnou rovnici zná každý. Méně lidí už ví, že rychlost světa je dána vlastnostmi vakua - permitivitou a permeabilitou. Je zajímavé, že vakuum vůbec nějaké vlastnosti má.
A je dvojnásob zajímavé, že tedy tyto vlastnosti vakua určují, kolik (klidové) energie hmota obsahuje. Mohou být tedy i jiná vakua než to "naše".
Současná kosmologie tvrdí, že se těsně po Velkém třesku vesmír nafouknul tzv. inflací asi 10^26 krát. Jak se to dalo udělat bez změny vlastností vakua a tedy i rychlosti světla v tom vakuu je mi záhadou.
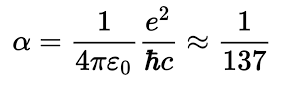
Alfa, pojmenovaná jako konstanta jemné struktury je jedna z největších záhad fyziky. Mnohokrát se objevuje v rovnicích kvantové mechaniky a elektrodynamiky aniž by bylo jasné, co přesně
reprezentuje. Sama je bezrozměrná, ale svazuje několik základních fyzikálních konstant našeho vesmíru.
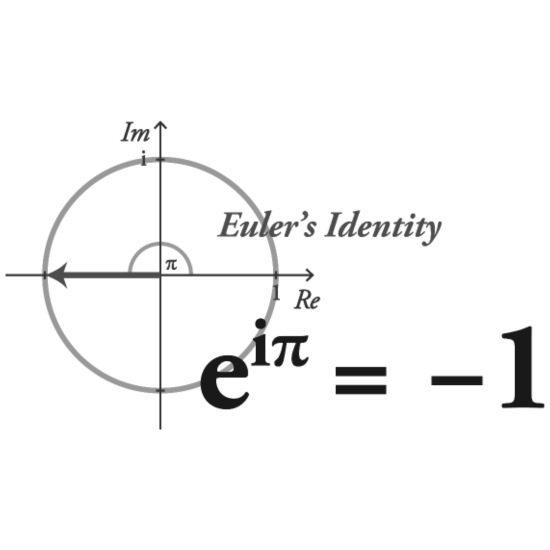
Eulerova formule ukazuje, že běžné představy o tom co je a není možné jsou vlastně jen silou zvyku a pro vesmír pramálo znamenají. Imaginární mocnina kladného čísla je záporné reálné číslo, hm.
Opačnou cestou je samozřejmě "i" coby odmocnina z -1.
Vlnová funkce jenž je řešením Schrödingerovy rovnice má pro výskyt částice v reálném prostoru ryze imaginární řešení.
Z Wiki: Schrödingerova rovnice určuje chování vlnové funkce, avšak neurčuje, co vlastně vlnová funkce je (!!!). Interpretaci vlnové funkce jako amplitudy pravděpodobnosti předložil v roce 1926 Max Born.
Jsou však i jiné interpretace kvantové mechaniky.
Feigenbaumova konstanta
Vyjadřuje (zjednodušeně řečeno), že velmi široká skupina jevů (biologických, fyzikálních, ekonomických, logistických, společenských...) přechází z uspořádaného stavu do chaosu stejnou "rychlostí zdvojnásobení
chaosu" kterou vyjadřuje právě tato konstanta.
Ramanujanova sumace
Ramanujan vymyslel, že když se zjevně divergentní suma s nekonečným součtem zapíše jako součet několika speciálních sum a s nimi se provedou výpočty využívající paradoxů nekonečna, vyjde jako suma konečné číslo.
Překvapivě to má matematická i fyzikální využití, pro řadu vědců samozřejmě velmi sporná. Zřejmě se takto jeden matematický hřích vytlouká druhým.
Zpět na úvodní stránku